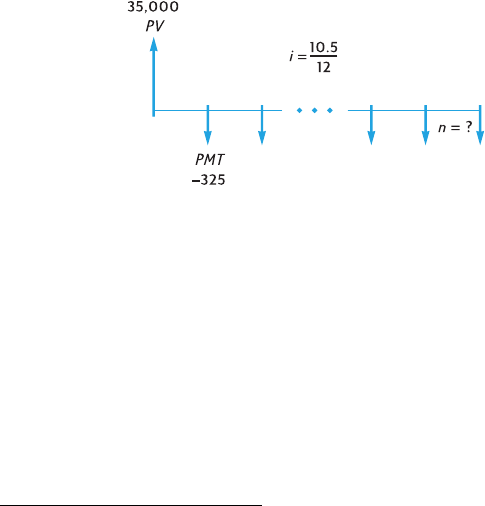
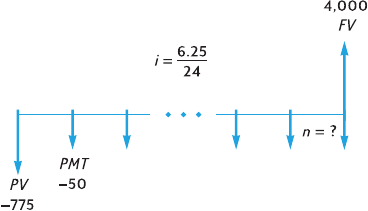
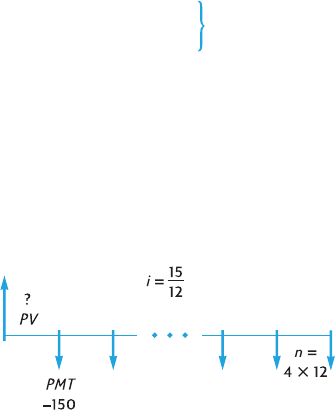
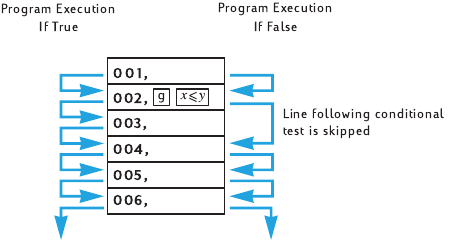
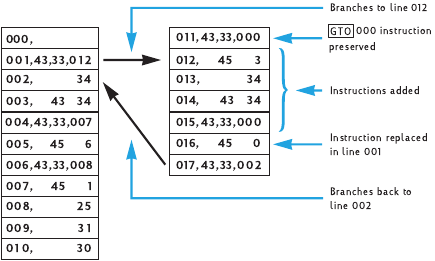
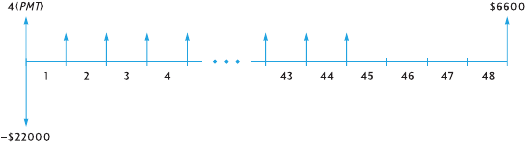
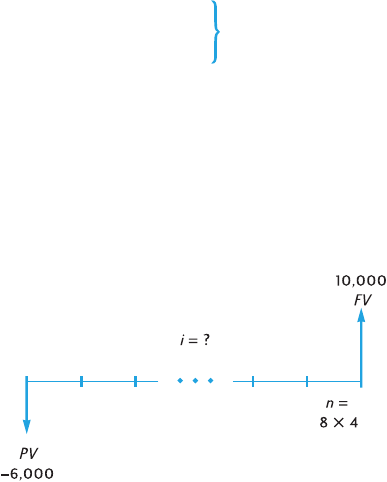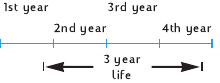Contents 9
Error 4: Memory.......................................................................................... 182
Error 5: Compound Interest........................................................................ 182
Error 6: Storage Registers.......................................................................... 183
Error 7: IRR ................................................................................................ 183
Error 8: Calendar........................................................................................ 184
Error 9: Service........................................................................................... 184
Pr Error ....................................................................................................... 184
Appendix E: Formulas Used ............................................................ 185
Percentage ................................................................................................. 185
Interest........................................................................................................ 185
Simple Interest...................................................................................... 185
Compound Interest............................................................................... 185
Amortization................................................................................................ 186
Discounted Cash Flow Analysis ................................................................. 187
Net Present Value ................................................................................ 187
Internal Rate of Return ......................................................................... 187
Calendar..................................................................................................... 187
Actual Day Basis .................................................................................. 187
30/360 Day Basis ................................................................................. 188
Bonds ......................................................................................................... 188
Depreciation ............................................................................................... 189
Straight-Line Depreciation.................................................................... 189
Sum-of-the-Years-Digits Depreciation.................................................. 190
Declining-Balance Depreciation ........................................................... 190
Modified Internal Rate of Return................................................................. 190
Advance Payments..................................................................................... 191
Interest Rate Conversions .......................................................................... 191
Finite Compounding ............................................................................. 191
Continuous Compounding.................................................................... 191
Statistics ..................................................................................................... 191
Mean..................................................................................................... 191
Weighted Mean .................................................................................... 192
Linear Estimation.................................................................................. 192
Standard Deviation............................................................................... 192
Factorial................................................................................................ 192
The Rent or Buy Decision........................................................................... 193
Appendix F: Battery, Warranty, and Service Information ........ 195
Battery ........................................................................................................ 195
Low-Power Indication ................................................................................. 195
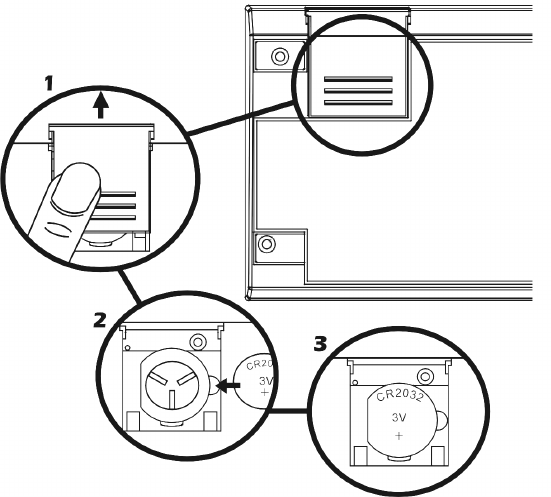
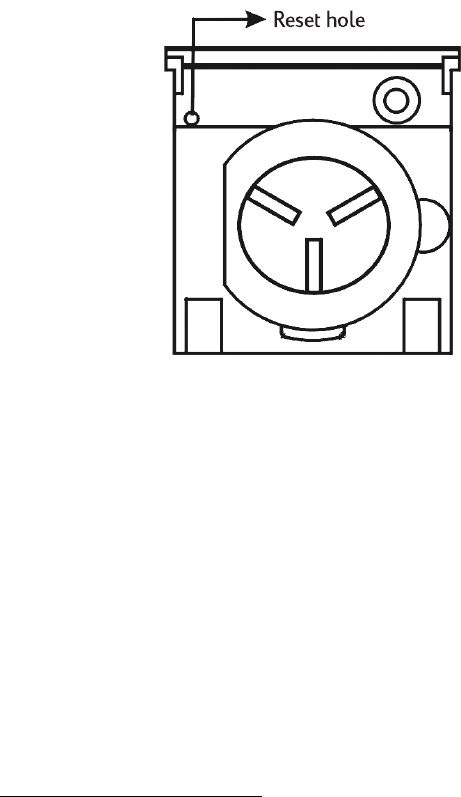
Installing a New Battery........................................................................ 195
Verifying Proper Operation (Self-Tests) ..................................................... 196
Warranty ..................................................................................................... 198
Service........................................................................................................ 200
Potential For Radio/Television Interference (for U.S.A. Only) .................... 201
Temperature Specifications........................................................................ 201
Noise Declaration ....................................................................................... 201
Regulation applying to The Netherlands .................................................... 202